MLOps
Your Center of Excellence for Machine Learning Operations and Production AI
Your Models Were Accurate Yesterday. What About Today?
In a volatile world, your machine learning models can turn quickly from assets into liabilities. When faced with conditions not encountered in the training data, your models will make inaccurate and unreliable predictions that will undermine consumer trust and introduce risk to the business. Additionally, most machine learning deployment processes today are manual, complex, and span data science, business, and IT organizations impeding the rapid detection and repair of model performance problems.
To maintain current levels of AI adoption and scale in order to take advantage of new opportunities, every organization needs a better way to deploy and manage the lifecycle of all their production models holistically across the enterprise.
DataRobot MLOps provides a center of excellence for your production AI. This gives you a single place to deploy, monitor, manage, and govern all your models in production, regardless of how they were created or when and where they were deployed.
Try it Now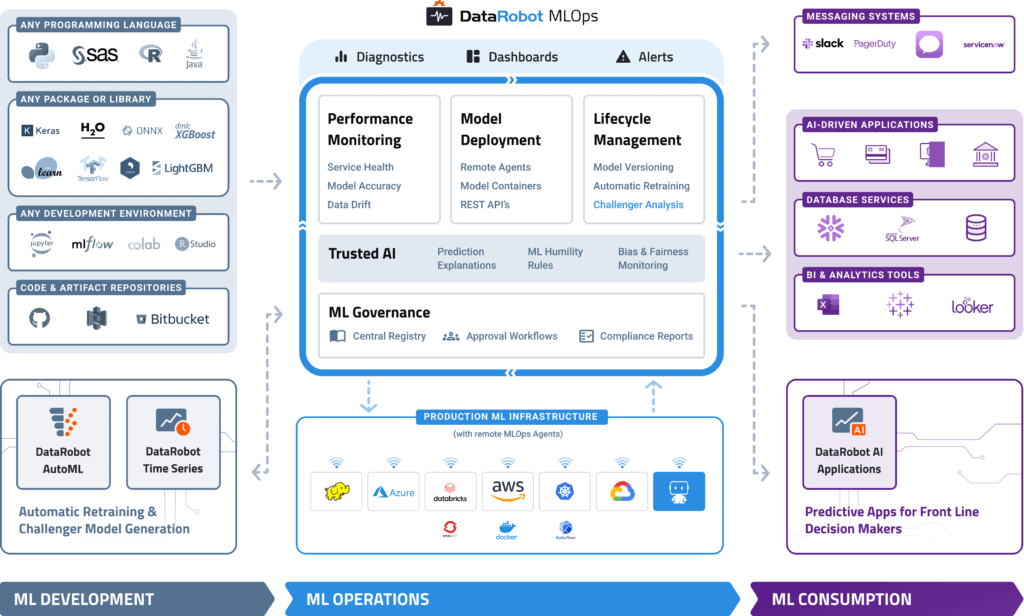
Monitor Your Existing Models in Just a Few Lines of Code
You can quickly configure your existing models to work with MLOps regardless of how they were built or where they are deployed. In just a few lines of code, you will get instant access to advanced ML monitoring built on a robust governance framework to manage the lifecycle of all your production AI.
Build and Run Your Models Anywhere
With MLOps, you can easily deploy any model to your production environment of choice, on-prem, in the cloud, or hybrid. By instrumenting MLOps monitoring agents, you can add monitoring to any existing production model already deployed.
MLOps makes it easy to deploy models written in any open-source language or library and expose a production-quality, REST API to support real-time or batch predictions. MLOps also offers built-in, write-back integrations to systems such as Snowflake and Tableau.
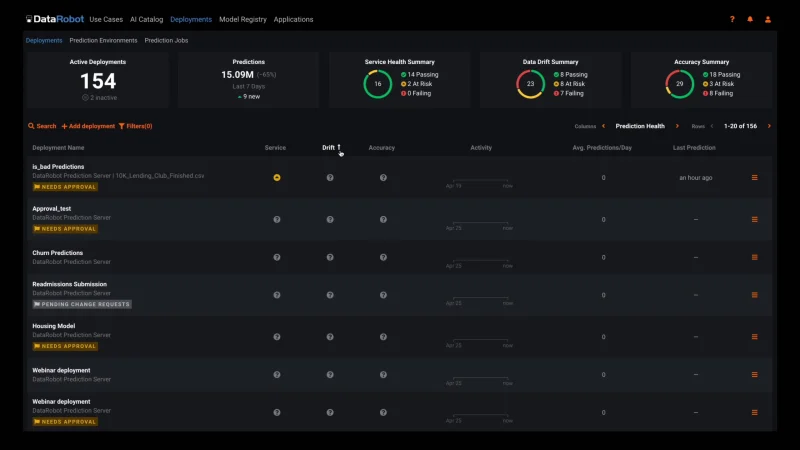
Automated Model Health Monitoring and Lifecycle Management
MLOps provides constant monitoring and production diagnostics to improve the performance of your existing models. Best practice ML monitoring right out of the box enables you to track service health, accuracy, and data drift to explain why your model is degrading. Build your own challenger models or use our industry-leading AutoML product to build and test them for you. MLOps gives you constant evaluation and continuous learning capabilities that allow you to avoid surprise changes in model performance down the road — a situation becoming only too familiar in today’s dynamic and volatile world.
Embedded Governance, Humility, and Fairness
MLOps establishes a framework that helps to maintain the governance process for your AI projects across your entire organization. With customizable governance policies, you will have complete control over the access, review, and approval workflows. It will also allow you to access the history of prediction activity and model updates for regulatory compliance. This means you always know what models have been created, as well as how they are used and updated.
With the Humility feature, you can configure rules that enable models to recognize, in real-time, when they make uncertain predictions. Check out MLOps 101 by DataRobot to learn more.
MLOps 101: The Foundation for Your AI Strategy
Machine Learning Operations (MLOps) allows organizations to alleviate many of the issues on the path to AI with ROI by providing a technological backbone for managing the machine learning lifecycle through automation and scalability. Check out this MLOps guide by DataRobot.
Get the Guide